Graf svake funkcije je numeriran. Pobudova rasporedi online. Ravna linija koja prolazi kroz danu točku, paralelna sa danim vektorom

Yakshcho roztashuvati jedan numerički broj koordinatna ravnina, tada za ovu točku možete pronaći koordinate. Poredaj brojčano tako da joj središte bude poravnato s koordinatnom točkom ravnine, a to je točka O (0; 0).

Pozovite jedan numerički broj da označite točke koje označavaju klas na broju.

• četvrtine - 0 ili 2π, π/2, π, (2π)/3,
• sredina četvrtina - π/4, (3π)/4, (5π)/4, (7π)/4,
• trećine četvrtine - π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

Na koordinatnoj ravnini, s navedenom vrijednošću raspodjele pojedinog udjela na njoj, možete pronaći koordinate koje odgovaraju tim točkama udjela.

Koordinate krajeva četvrtina vrlo je lako pronaći. U točki 0, x koordinata je jednaka 1, a y koordinata je jednaka 0. Možete to napisati ovako: A (0) = A (1; 0).

Kraj prvog kvartala rasta je na pozitivnoj ordinati. Otže, B(π/2) = B(0; 1).

Kraj druge četvrtine nalazi se na negativnoj strani apscisa: C(π) = C(-1; 0).

Kraj treće četvrtine: D((2π)/3) = D(0; -1).

Kako znaš koordinate sredine četvrti? Za koga će biti trikutnik ravnog kroja. Njegova hipotenuza je presjek od središta udjela (ili početka koordinata) do sredine četvrtine udjela. Ovo je radijus udjela. Fragmenti su jednostruki, tada je hipotenuza jednaka 1. Zatim povucite okomicu iz točke udjela na bilo koju os. Možeš li dosegnuti x os. Unesite ravno izrezani tricutnik, dovzhini noge od kojih - x i y koordinate točke udjela.

Postavite četvrtinu udjela na 90º. I pola četvrtine postaje 45º. Fragmenti hipotenuze povlače se do točke sredine četvrtine, tada udaljenost između hipotenuze i noge koja izlazi iz koordinatne baze doseže 45º. Ale suma kutiv be-yaky trikutnik dorivnyuya 180 º. Pa, između hipotenuze i druge katete izgubljeno je 45º. Izlazi tricutnik ravnog kroja, ravnog kroja.

Iz Pitagorinog teorema možemo ukloniti jednadžbu x 2 + y 2 = 12. Ako je x = y i 1 2 = 1, tada će se jednadžba svesti na x 2 + x 2 = 1. Nakon što smo to pronašli, možemo uklonite x = √½ = 1/√2 = √2/2.

Dakle, koordinate točke su M 1 (π/4) = M 1 (√2/2; √2/2).

Na koordinatama točaka središnjih točaka ostalih četvrtina mijenjat će se samo znakovi, a moduli će izgubiti iste vrijednosti, a pravokutni trokut samo će biti obrnut. Odbijamo:
M 2 ((3π)/4) = M 2 (-√2/2; √2/2)
M 3 ((5π)/4) = M 3 (-√2/2; -√2/2)
M 4 ((7π)/4) = M 4 (√2/2; -√2/2)

Ako se zadaju koordinate trećih dijelova četvrtine udjela, postojat će i pravocrtni trikot. Ako uzmete točku π/6 i povučete okomicu na x-os, tada presjek između hipotenuze i kraka koji leži na x-osi postaje 30º. Jasno je da leži nasuprot kutu na 30º, što je ista polovica hipotenuze. Pa, znali smo da je koordinata y pobijedila ½.

Znajući da je hipotenuza jedne od kateta poznata, prema Pitagorinom poučku znamo i drugu katetu:
x 2 + (½) 2 = 1 2
x 2 = 1 - ¼ = ¾
x = √3/2

Dakle, T 1 (π/6) = T 1 (√3/2; ½).

Za točku druge trećine prve četvrtine (π/3), povucite okomicu na y-os što je točnije moguće. Tada će koordinate na početku također biti 30º. Ovdje je koordinata x veća od ½, a y je veća od √3/2: T 2 (π/3) = T 2 (½; √3/2).

Za ostale točke trećine i četvrtine mijenjaju se znakovi i redoslijed vrijednosti koordinata. Sve točke koje su najbliže x osi nalazit će se iza modula vrijednosti x koordinate, koja je jednaka √3/2. One točke koje su najbliže y osi nalaze se iza modula y vrijednosti, koji je jednak √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)

Analitička geometrija, međutim, pruža nove metode za rješavanje geometrijskih problema. U tu se svrhu sve navedene točke i pravci pridružuju jednom koordinatnom sustavu.

U koordinatnom sustavu kožnu točku možemo okarakterizirati svojim koordinatama, a kožnu liniju možemo okarakterizirati s dvije nepoznate koordinate, graf čija je linija. Na taj se način geometrijski problem svodi na algebarski, pri čemu su sve metode proračuna dobro uvježbane.

Postoji geometrijska točka iste snage (kožna točka kolca jednako je udaljena od jedne točke, koja se naziva središte). Ulog ljubomore može imitirati ovu moć, zadovoljiti ovaj um.

Geometrijska interpretacija udjela u razini je cijela linija udjela.

Ako ulog postavite u koordinatni sustav, tada sve točke udjela padaju unutar istog uma - kretanje od njih do središta udjela može biti isto i jednako udjelu.

Kolo sa središtem blizu točke A i radijus R mogu se postaviti u koordinatnu ravninu.

Kako koordinirati do centra (a; b) , i koordinate bilo koje iscrtane točke (x;y) , onda tirkizni kolac izgleda ovako:

Kako je kvadrat polumjera kočića jednak zbroju kvadrata, razlika između različitih koordinata bilo koje točke kočića i središta jednaka je jednakosti kočića u ravnom koordinatnom sustavu.

Ako je središte kočića blizu koordinirajuće točke, tada je kvadrat polumjera kočića jednak zbroju kvadrata koordinata bilo koje točke kočića. U čijem slučaju se pojavljuje ražena kola:

Oh dobro, hajde geometrijski lik Kao geometrijsko mjesto, točka je pridružena jednakima, koji povezuju koordinate svoje točke. I iznenađenje, poravnanje koje povezuje koordinate x і na , Pravac je definiran kao geometrijsko mjesto točaka ravnine, čije koordinate odgovaraju ovoj ravnini.

Prijavite se za zadatke udjela Rivnyanya

Zavdannya. Preferencije danog uloga

Presavijte ravni kolac sa središtem u točki O (2;-3) i radijusom 4.

Odluka.
Vratimo se formuli:
R 2 = (x-a) 2 + (y-b) 2

Zamijenimo značenje formule.
Cola radijus R = 4
Koordinate do centra uloga (iznimno blizu pameti)
a = 2
b = -3

Zanemarljivo:
(x - 2) 2 + (y - (-3)) 2 = 4 2
ili drugo
(x - 2) 2 + (y + 3) 2 = 16.

Zavdannya. Chi laž točka rívnyannya ulog

Provjerite što učiniti, točka A(2;3) Rivnyanyu kolac (x - 2) 2 +(y+3) 2 = 16 .

Odluka.
Ako je točka postavljena na kolu, njezine koordinate odgovaraju poravnanju kruga.
Da bismo provjerili da li se točka kočića nalazi na zadanim koordinatama, zamijenimo koordinate točke u koordinatama datog kočića.

U Rivnanji ( x - 2) 2 + (g + 3) 2 = 16
zamijenimo, dakle, iza mozga koordinate točke A(2;3).
x = 2
y=3

Provjerimo istinitost poricane jednakosti
(x - 2) 2 + (g + 3) 2 = 16
(2 - 2) 2 + (3 + 3) 2 = 16
0 + 36 = 16 ljubomora je pogrešna

Na ovaj način je postavljena točka nemojte odugovlačiti s dobrodošlicom danu razinu uloga.

Kolom Točka ravnine koja je jednako udaljena od te točke naziva se središtem.

Kako je točka C središte kočića, R je radijus, a M dovoljna točka kočića, tada je kolac

Ljubomora (1) ê Rivnyannaya kolac radijus R od središta u točki C.

Neka je ravnini zadan pravokutni Kartezijev koordinatni sustav (sl. 104) i točka C( A; b) - Središte udjela radijusa R. Nekhai M( X; na) - dovoljna točka ovog uloga.

Oskolki |SM| = \(\sqrt((x - a)^2 + (y - b)^2) \), tada se jednadžba (1) može napisati na sljedeći način:

\(\sqrt((x - a)^2 + (y - b)^2) \) = R

(x-a) 2 + (y - b) 2 = R 2 (2)

Rivnyannya (2) poziv na Zagalnym Rivnyany kolac ili u redove udjela radijusa R sa središtem u točki ( A; b). Na primjer, ljubomora

(x - l) 2 + ( g + 3) 2 = 25

Postoji libela polumjera R = 5 sa središtem u točki (1; -3).

Kako se središte udjela približava zrnu koordinata, pojavljuje se poravnanje (2).

x 2 + na 2 = R2. (3)

Rivnyannya (3) poziv kanonski vladari na kolac .

Zavdannya 1. Napišite razinu polumjera R = 7 sa središtem na koordinatama.

Uklanja se bescentrična zamjena vrijednosti radijusa u razini (3).

x 2 + na 2 = 49.

Zavdannya 2. Napišite liniju radijusa R = 9 sa središtem u točki C (3, -6).

Zamjenom vrijednosti koordinata točke C i vrijednosti polumjera u formuli (2), možemo ukloniti

(x - 3) 2 + (na- (-6)) 2 = 81 ili ( x - 3) 2 + (na + 6) 2 = 81.

Zavdannya 3. Pronađite središte i radijus udjela

(x + 3) 2 + (na-5) 2 =100.

Jednako tako s obzirom na razinu uloga (2), što je najvažnije, A = -3, b= 5, R = 10. Otje, C(-3; 5), R = 10.

Zavdannya 4. Ponesi tu ljubomoru

x 2 + na 2 + 4x - 2g - 4 = 0

ê u redove kolca. Pronađite središte i radijus.

Pomirimo lijevi dio ove ljubomore:

x 2 + 4x + 4- 4 + na 2 - 2na +1-1-4 = 0

(x + 2) 2 + (na - 1) 2 = 9.

Središte je središte kruga u točki (-2; 1); Radijus kočića je veći od 3.

Zavdannya 5. Napišite ravnu liniju sa središtem u točki C(-1; -1), koja je ravna linija AB, kao što je A (2; -1), B(- 1; 3).

Napišimo ravno AB:

ili 4 x + 3g-5 = 0.

Fragmenti se sudaraju s ovom ravnom linijom, tada je radijus prijelaza do točke torzije okomit na ovu ravnu liniju. Da biste odredili radijus, morate znati udaljenost od točke C(-1; -1) - središta kola do ravne crte 4 x + 3g-5 = 0:

Napišimo zakivanje kolca šukane

(x +1) 2 + (g +1) 2 = 144 / 25

Prijeđimo na pravokutni koordinatni sustav x 2 + na 2 = R2. Pogledajmo dovoljnu točku M( X; na) (Slika 105).

Idemo radijus vektor OM> točka M stvara rez veličine t s pozitivnom ravnom osi x, tada apsciza i ordinata točke M mijenjaju položaj od t

(0 t x i y kroz t, znamo

x= Rcos t ; g= R sin t , 0 t

Rivnyannya (4) se zovu parametarska poravnanja udjela sa središtem na vrhu koordinata.

Zavdannya 6. Kružnica je dana linijama

x= \(\sqrt(3)\)cos t, g= \(\sqrt(3)\)sin t, 0 t

Zabilježite kanonski rang ovog udjela.

Moj um vibrira x 2 = 3 cos 2 t, na 2 = 3 grijeh 2 t. Dodavanje jednakosti, pojam po pojam, uklonjivo

x 2 + na 2 = 3 (cos 2 t+ grijeh 2 t)

ili drugo x 2 + na 2 = 3

Vrijednost 1. Brojčano sve ( brojevni pravac, koordinatni pravac) Ox je pravac u kojem se nalazi točka O klip klipa (kob koordinata)(slika 1), izravno

O → x

naznačeno kao pozitivna režija i označen je odsjek, čiji se dowzhin prihvaća kao dovzhini jedan.

Vrijednost 2. Rez u kojem se dovzhin uzima kao jedan dovzhin naziva se ljestvica.

Točka kože na numeričkoj osi je koordinata koja je govorni broj. Koordinata točke O jednaka je nuli. Koordinata prethodne točke A, koja leži na razmjeni Ox, jednaka je prethodnoj dionici OA. Koordinata najviše točke A numeričke osi koja ne leži na zamjeni Ox je negativna, au apsolutnoj vrijednosti jednaka je posljednjem presjeku OA.

Vrijednost 3. Pravokutni Kartezijev koordinatni sustav Oxy na ravnini nazvati dva imena zajedno okomito numeričke osi Ox i Oy međutim, u različitim razmjerimaі s klipom klipa u točki O, osim toga, tako da se zaokret od zamjene Ox do zaokreta za 90° do zamjene Oy događa ravno naprijed suprotno od smjera strelice obljetnice(slika 2).

Poštovanje. Pravokutni Kartezijev koordinatni sustav Oxy, prikazan kao beba 2, zove se desni koordinatni sustav, upravi lijevi koordinatni sustavi, Kada okrenete Ox na kut od 90° prije promjene Oy, pomiče se ravno u smjeru strelice godine. Čijeg svjedoka imamo? gledano iz desnog koordinatnog sustava, bez raspravljanja o bilo čemu posebnom.

Ako u ravninu uvedemo sustav pravocrtnih kartezijevih koordinata Oxy, tada se točka ravnine povećava dvije koordinate – apscisі ordinata, koji se računaju s takvim rangom. Neka je A dovoljna točka ravnine. Spustimo okomice iz točke A A.A. 1 i A.A. 2 na ravnoj liniji Ox i Oy u liniji (sl. 3).

Vrijednost 4. Apscisa točke A je koordinata točke A 1 na numeričkoj osi Ox, ordinata točke A je koordinata točke A 2 na numeričkoj osi Oy.

Ugovoreni sastanak. Koordinate (apscis i ordinata) točke A za pravokutni Kartezijev koordinatni sustav Oxy (slika 4) ima prihvaćenu vrijednost A(x;g) ili drugo A = (x; g).

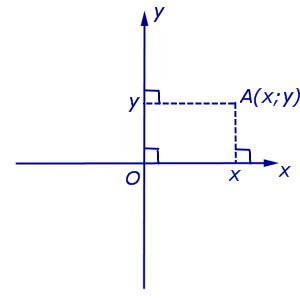
Poštovanje. Točka O, tzv kob koordinata, svibnja koordinate O(0 ; 0) .

Vicenzacija 5. U pravokutnom Kartezijevom koordinatnom sustavu Oxy brojčana cjelina Ox naziva se cijeli apscis, a numerička cjelina Oy cijela ordinata (sl. 5).

Vicenzacija 6. Koža ima pravokutni kartezijanski koordinatni sustav koji dijeli područje na 4 četvrtine (kvadranta), čije je numeriranje prikazano malim 5.

Vicenza 7. Područje na kojem je zadan pravokutni Kartezijev koordinatni sustav naziva se koordinatna ravnina.

Poštovanje. Cijela apscisa određena je na koordinatnoj ravnini razina g= 0, cijela ordinata određena je na koordinatnoj ravnini razina x = 0.

Tverzhennia 1. Stanite između dvije točke koordinatna ravnina

A 1 (x 1 ;g 1) і A 2 (x 2 ;g 2)

biti izračunat iza formule

Gotovo. Pogledajmo sliku 6.