Predstavljanje osnovnih trigonometrijskih formula i osnovnih supstitucija. Prikazane su metode integriranja trigonometrijskih funkcija - integracija racionalnih funkcija, zbrajanje statičkih funkcija oblika sin x i cos x, zbrajanje bogatog člana, eksponent sinusa i kosinusa, integracija povratnih trigonometrijskih funkcija y. U igru ​​su ušle nestandardne metode.

Zmist

Standardne metode integriranja trigonometrijskih funkcija

Zagalni pristup

Prvo, ako je potrebno, integralni izraz treba preurediti tako da trigonometrijske funkcije leže u jednom argumentu, što se može izbjeći bez integracije varijabli.

Na primjer, ako se nalazi integralni virus sin(x+a)і cos(x+b), trag visconatijeve rekreacije:
cos(x+b) = cos(x+a - (a-b)) = cos (x+a) cos (b-a) + grijeh ( x+a ) grijeh (b-a).
Zatim izvršite zamjenu z = x + a. Kao rezultat toga, trigonometrijske funkcije više nisu podložne integraciji varijable z.

Ako trigonometrijske funkcije leže u jednom argumentu, što se izbjegava integracijom varijable (dopušteno sa z), tada je integralni izraz sastavljen samo od funkcije tipa grijeh z, jer z, tg z, ctg z, tada morate napraviti zamjenu
.
Ova supstitucija dovodi do integracije racionalnih i iracionalnih funkcija (što je korijenska funkcija) i omogućuje nam izračunavanje integrala koji se može integrirati u elementarne funkcije.

Međutim, često možete pronaći druge metode koje vam omogućuju izračunavanje integrala na kraći način, ovisno o specifičnostima integralnog izraza. U nastavku je sažetak glavnih takvih metoda.

Metode integriranja racionalnih funkcija sin x i cos x

Racionalne funkcije iz grijeh xі cos x- ova funkcija stvorena s grijeh x, cos x A postoje neke konstante iza dodatne operacije zbrajanja, oduzimanja, množenja i time dovođenja na cjelovitu razinu. Smrdovi su označeni na sljedeći način: R (sin x, cos x). To može uključivati ​​tangente i kotangense, fragmente nastale dijeljenjem sinusa na kosinus i slično.
Integrali racionalnih funkcija izgledaju ovako:
.

Metode za integriranje racionalnih trigonometrijskih funkcija su sljedeće.
1) Supstitucija se prvo dovodi do integrala racionalni razlomak. Međutim, u nekim situacijama postoje zamjene (one su prikazane u nastavku) koje dovode do kraćih izračuna.
2) Yakscho R (sin x, cos x) cos x → - cos x grijeh x.
3) Yakscho R (sin x, cos x) pomnožite s -1 prilikom zamjene sin x → - sin x, tada je supstitucija t = cos x.
4) Yakscho R (sin x, cos x) ne mijenja kao u jednosatnoj zamjeni cos x → - cos x, і sin x → - sin x, tada je supstitucija t = tg x ili t = ctg x.

primijeniti:
, , .

Zbrajanje statičkih funkcija u cos x i sin x

Integrali uma

ê integrali iz racionalnih trigonometrijskih funkcija. Stoga se metode mogu koristiti u prethodnom odjeljku. U nastavku se raspravlja o metodama koje se temelje na specifičnostima takvih integrala.

Kako su m i n racionalni brojevi, tada je jedna od zamjena t = grijeh x ili t = cos x integral se svodi na integral iz diferencijalnog binoma.

Budući da su m i n cijeli brojevi, integracija se može izvršiti pomoću dodatnih redukcijskih formula:

;
;
;
.

stražnjica:
.

Integrali za stvaranje mnogih članova sinusa i kosinusa

Integrali oblika:
, ,
gdje je P(x) polinom od x, koji se može integrirati po dijelovima. To dovodi do sljedećih formula:

;
.

primijeniti:
, .

Integrali iz stvaranja bogatog člana, eksponencijala sinusa i kosinusa

Integrali oblika:
, ,
gdje je P(x) bogati član u x, može se integrirati pomoću Eulerove formule
e iax = cos sjekira + isin sjekira(de i 2 = - 1 ).
U tu svrhu, metodom prikazanom u prvoj točki, izračunavamo integral
.
Nakon što smo vidjeli aktivni i očiti dio rezultata, možemo izvesti izlazne integrale.

stražnjica:
.

Nestandardne metode integriranja trigonometrijskih funkcija

Dolje je niz nestandardnih metoda koje vam omogućuju da viskonirate i pojednostavite integraciju trigonometrijskih funkcija.

Duljina gledanja (a sin x + b cos x)

Ako je integrativni virus pohranjen samo u a sin x + b cos x, onda je lijepo postaviti formulu:
,
de.

Na primjer

Rastavljanje razlomka iz sinusa i kosinusa na proste razlomke

Pogledajmo integral
.
Najjednostavnija metoda integracije leži u nesavijenom razlomku na jednostavan, stagnirajući način:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integracija prve pozornice

Pri računanju integrala
,
lako je vidjeti cijeli dio kadra i marša transparenta
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)' .
Kontinuirani A i B nastaju zbog poravnanja lijevog i desnog dijela.

Wikorystan književnost:
N.M. Gunther, R.O. Kuzmin, Zbirka knjiga velike matematike, "Lan", 2003.

div. također:

Integrali kao trigonometrijske funkcije.
Primijenite svoju odluku

U ovoj lekciji smo pogledali integrale trigonometrijskih funkcija, tako da će popuna integrala biti sinus, kosinus, tangens i kotangens za razne kombinacije. Svi opušci bit će detaljno prikazani, čajniku dostupni i razumljivi.

Da biste uspješno integrirali integrale u trigonometrijske funkcije, morate dobro razumjeti najjednostavnije integrale, kao i druge metode integracije. S ovim materijalima možete se upoznati na predavanjima Bezvrijedni integral. Primijenite svoju odluku ta .

A sada nam treba: Tablica integrala, Tablica polazakaі Savjetnik trigonometrijskih formula. Brkovi metodički suputnici možete pronaći na stranici Matematičke formule i tablice. Preporučam da se sve zategne. Posebno ću se usredotočiti na trigonometrijske formule, smrad mučiti se buti ispred očima– bez kojih će se učinkovitost robota značajno promijeniti.

Prije svega o tim integralima u ovom članku ni. Ovdje nema integrala, - kosinus, sinus, pomnožen bilo kojim članom (ponekad s tangensom ili kotangensom). Takvi se integrali integriraju po dijelovima, a da biste naučili metodu, uzmite lekciju Integracija po dijelovima. Primijenite rješenje Također, ovdje nema integrala s “lukovima” - arktangens, arksinus itd., također se najčešće integriraju po dijelovima.

Za pronalaženje integrala iz trigonometrijskih funkcija koriste se brojne metode:

(4) Koristimo formula tablice , uniformnost, umjesto "X" imamo sklopivi izraz.

stražnjica 2

stražnjica 3

Znati nevrijednosni integral.

Klasik žanra za one raspoložene. Kao što ste možda primijetili, tablica integrala nema integral za tangens i kotangens, a o takvim integralima možete saznati.

(1) Vikoristova trigonometrijska formula

(2) Spajamo funkciju pod predznakom diferencijala.

(3) Vikorist stolni integral .

stražnjica 4

Nađi bezvrijedni integral.

Ovo je opušak za samostalnu odluku, izvan odluke i dokaza - kao lekcija.

stražnjica 5

Nađi bezvrijedni integral.

Naši koraci polako idu naprijed =).
Kao prvo:

(1) Vikoristova formula

(2) Vikorist fundamentalno trigonometrijski identitet , zašto vibrira? .

(3) Podijelite broj po pojam po pojam.

(4) Linearnost nevrijednog integrala određuje Vikorist.

(5) Integrirano korištenjem dodatne tablice.

stražnjica 6

Nađi bezvrijedni integral.

Ovo je opušak za samostalnu odluku, izvan odluke i dokaza - kao lekcija.

Postoje i integrali tangensa i kotangenata, koji se nalaze na višim razinama. Integral tangente na kub pregledan u lekciji Kako izračunati površinu ravne figure? Integrale tangensa (kotangensa) u četvrtom i petom koraku možete dobiti na stranici Preklopni integrali.

Donji stupanj integralne funkcije

Ova tehnika funkcionira kada su integralne funkcije napunjene sinusima i kosinusima momci korake. Za nižu razinu koristite trigonometrijske formule , Štoviše, preostala formula se često koristi u obrnutom smjeru: .

stražnjica 7

Nađi bezvrijedni integral.

Odluka:

U principu, nema tu ništa novo, osim što smo formulu zapisali (promjena stupnja subintegralne funkcije). Zahvalan sam što sam brzo donio odluku. U svijetu se akumulirani integral može lako pronaći, što štedi sat vremena i sasvim je prihvatljivo kod završetka zadatka. U tom slučaju nemojte u potpunosti zapisivati ​​pravilo Prvo uzimamo integral iz 1, zatim iz .

stražnjica 8

Nađi bezvrijedni integral.

Ovo je opušak za samostalnu odluku, izvan odluke i dokaza - kao lekcija.

Ovo su napredne faze:

stražnjica 9

Nađi bezvrijedni integral.

Prvo odluka, pa komentari:

(1) Možemo pripremiti integralnu funkciju za formuliranje formule .

(2) Formula Vlasne zastosov.

(3) Uzimamo predznak kvadrata i stavljamo konstantu u predznak integrala. Moglo bi se zaraditi malo drugačije, ali bi mi bilo lakše.

(4) Vikoristova formula

(5) Za treće zbrajanje ponovno spuštamo korak, a zatim koristimo dodatnu formulu .

(6) Rade se slični dodaci (ovdje sam ih podijelio dio po dio ta vikonav dodavannya).

(7) Uzimamo integral, pravilo linearnosti Ovaj način uvođenja funkcije pod diferencijalnim predznakom je jasno definiran.

(8) Dokaz je jasan.

! Za nedefinirani integral često je moguće napisati verziju naljepnice na sljedeće načine:

U zadnjici bi se rezidualni odgovor mogao napisati drugačije - otvorite ruke i počnite raditi prije integracije virusa, tako da kraj stražnjice bude potpuno prihvatljiv:

Sasvim je moguće da bi ova opcija bila bolja, samo ću to objasniti na isti način kao i sam zvuk). Osovina je još jedna karakteristična stražnjica za neovisnu vyrishenya:

stražnjica 10

Nađi bezvrijedni integral.

Ova se zadnjica može ispraviti na dva načina i možda ćete izaći dvije potpuno različite vrste(točnije, naizgled, smrdi izgledaju potpuno drugačije, a s matematičke točke gledišta su ekvivalentni). Bez obzira na sve, nećete naučiti najracionalniju metodu i patit ćete od otvaranja krakova, iskrivljenja drugih trigonometrijskih formula. Najučinkovitije rješenje temelji se na lekciji.

Predajte odlomak, napravite sažetak: imajte na umu bilo koju vrstu integrala , gdje ja - momci brojeva, čini se da je razina integralne funkcije niža.
Naime, integrali s 8 i 10 koraka su suženi, a njihova strahovita krvarenja riješena je višestrukim snižavanjem razine, a rezultati su dali dugoročne rezultate.

Metoda zamjene

Kao što je statistika već pogodila Metoda zamjene varijable u neidentificiranom integralu Glavni razlog za odabir metode supstitucije je taj što integrand ima sličnu funkciju:
(funkcije koje ne moraju nužno postojati u kreaciji)

stražnjica 11

Nađi bezvrijedni integral.

Prikazane u tablici povezanih i označenih formula, , tada naš integralni izraz ima istu funkciju. No, važno je da se diferenciranjem kosinus i sinus međusobno transformiraju jedan po jedan, te se javlja problem: kako zamijeniti varijablu i što se podrazumijeva pod - sinusom i kosinusom?! Prehranu je moguće odrediti znanstvenom metodom: ako napravimo pogrešne promjene, od toga neće biti ništa dobro.

Konačni orijentir: u sličnim situacijama potrebno je odrediti funkciju bivanja u znaku.

Rješenje se revidira i vrši se zamjena

S našim barjakom je sve u redu, sve je dugo ležalo, sad nemamo pojma što da radimo.
Za koje znamo razliku:

Ili ukratko:
Na temelju pravila proporcije potreban nam je sljedeći izraz:

Otje:

Sada su svi integralni izrazi samo u našim rukama i možemo nastaviti donositi odluke

Spreman. Dopustite mi da vas podsjetim što zamijeniti - oprostite integralnom virusu, u kojem je sve dovelo do integracije funkcije snage iza stola.

Nisam tako pedantno slikao ovu stražnjicu, ali to je učinjeno metodom ponavljanja i konsolidacije materijala za lekciju Metoda zamjene varijable u neidentificiranom integralu.

A sada dva gunda za samostalan nastup:

stražnjica 12

Nađi bezvrijedni integral.

stražnjica 13

Nađi bezvrijedni integral.

Više rješenja i sličnosti s lekcijom.

stražnjica 14

Nađi bezvrijedni integral.

Ovdje opet u integralnom izrazu postoje sinus i kosinus (funkcija s uzgrednom), ali i u tvorbi, te se postavlja dvojba - što podrazumijevamo pod sinusom i kosinusom?

Možete pokušati izvršiti zamjenu znanstvenom metodom, a ako se ništa ne pojavi, dodijelite je drugoj funkciji, drugim riječima:

Skriveni orijentir: potrebno je prepoznati funkciju koja se, figurativno, čini u “nemanuelnom položaju”.

Bitno je da u ovoj primjeni učenikov kosinus "pati" na koraku, a sinus sjedi tako, sam.

Pa napravimo zamjenu:

Ako netko ima poteškoća s algoritmom za zamjenu varijable i pronalaženje diferencijala, neka se vrati na lekciju Metoda zamjene varijable u neidentificiranom integralu.

stražnjica 15

Nađi bezvrijedni integral.

Analizirajmo integralnu funkciju, što treba označiti kao ?
Pogodimo naše znamenitosti:
1) Funkcija, koja je odgovorna za sve, poznata je barjaktaru;
2) Funkcija je u "neručnom položaju".

Prije svega, ove smjernice su iste kao i za trigonometrijske funkcije.

Ako su oba kriterija (osobito drugi kriteriji) zadovoljeni sinusom, potrebna je zamjena. U principu, zamjena se već može izvršiti, ali to bi bilo loše za početak, ali što učiniti s tim? Prije svega, "odaberemo" jedan kosinus:

Rezerviramo za naš "možda" diferencijal

I okreće se kroz sinus pomoću glavnog trigonometrijski identitet:

Sada se mijenja osovina:

Zagalne pravilo: U integralnoj funkciji nalazi se jedna od trigonometrijskih funkcija (sinus ili kosinus). nesparen stupnju, tada morate "uzorkovati" jednu funkciju iz neuparenog stupnja, a zatim dodijeliti drugu funkciju. Razgovarajmo o integralima, kosinusima i sinusima.

U slučaju koji smo promatrali s neuparenim svijetom, pronašli smo kosinus, pa smo uklonili jedan kosinus iz koraka i označili sinus.

stražnjica 16

Nađi bezvrijedni integral.

Koraci idu na zlit =).
Ovo je primjer neovisne odluke. Iznad svega, postoji rješenje i zaključak lekcije.

Univerzalna trigonometrijska supstitucija

Univerzalna trigonometrijska supstitucija najčešća je varijanta metode supstitucije. Možete pokušati sa stagnacijom ako ne znate što učiniti. Ali doista postoje neke smjernice za njegovu stagnaciju. Tipični integrali koji zahtijevaju univerzalnu trigonometrijsku zamjenu su sljedeći integrali: , , , itd.

stražnjica 17

Nađi bezvrijedni integral.

Univerzalna trigonometrijska supstitucija često se provodi na ovaj način. Zamijenimo: . Ne koristim slovo, nego slovo, što nije pravilo, ja to jednostavno tako znam.

Ovdje je razlika važnija, za koju ću, pošteno radi, reći:
Najvažniji arktangens na uvrijeđenom dijelu:

Arktangens i tangens se međusobno smanjuju:

Na ovaj način:

U praksi, ne morate ga slikati tako detaljno, već jednostavno skicirajte rezultat:

! Izraz je jedino fer jer ispod sinusa i kosinusa jednostavno imamo "ix" za integral (o tome ćemo kasnije) sve će biti malo drugačije!

Prilikom zamjene sinusa i kosinusa transformiramo u sljedeće razlomke:
, , koji se temelje na poznatim trigonometrijskim formulama: ,

Dakle, konačni dizajn može biti ovakav:

Provedimo univerzalnu trigonometrijsku zamjenu:

Postojat će upute za samostalni razvoj, sve dok se takve vrste ne mogu pregledati.

Integralni izraz može se pretvoriti iz stvaranja trigonometrijskih funkcija u zbroj

Pogledajmo integrale u kojima se integralna funkcija sastoji od sinusa i kosinusa prvog stupnja kao x, pomnoženih različitim faktorima, tako da možemo integrirati oblik

Brzo naučivši neke trigonometrijske formule

(2)
(3)
(4)
moguće je transformirati kožu iz kreacija u integralima oblika (31) u algebarski zbroj i integrirati iza formula

(5)

(6)

guza 1. Znati

Odluka.

Slijedeći formulu (2) na Znati guza 2.

integral trigonometrijske funkcije

Odluka. Znati guza 2.

Slijedeći formulu (3) na stražnjica 3.

Odluka.

Slijedeći formulu (4) na

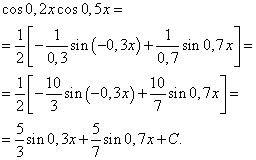
Očekuje se početak transformacije integralnog virusa:

(7)

Zastosovuyu formula (6), eliminiran Integral koraka sinusa i kosinusa istog argumenta Pogledajmo sada integral funkcije za stvaranje dva stupnja sinusa i kosinusa istog argumenta. U nizu epizoda jedan od izlagača ( m

ili drugo n) može se dodati nuli. n ) .

Pri integraciji takvih funkcija postaje jasno da se zajednički stupanj kosinusa može izraziti kroz sinus, a diferencijal sinusa jednak cos. Integral koraka sinusa i kosinusa istog argumentaі U nizu epizoda jedan od izlagača ( x dx

(ili se jednaki stupanj sinusa može izraziti kroz kosinus, a diferencijal kosinusa je isti - sin U nizu epizoda jedan od izlagača ( = 2Sljedeći su podijeljeni u dvije vrste: 1) Želio bih jedan od indikatora nesparen; 2) ofenzivni prikazi dečki.

Neka se ne dogodi prva epizoda, već sama emisija k+ 1 – nespareno. Todi, doktori, što Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene t k= grijeh Integral koraka sinusa i kosinusa istog argumenta x Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene Odluka je smanjiti integraciju bogatih članova tijela Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene. Zašto nemaš više koraka? k neuparen, zatim ga popravite na sličan način, gledajući multiplikator sin Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene, određujući rješenje integralne funkcije kroz cos i s poštovanjem =cos . Ova tehnika se može koristiti u Integracija privatnih stupnjeva sinusa i kosinusa , ako Volio bih da jedan od izlagača bude nesparen

. Sve pohvale idu onome tko Integral koraka sinusa i kosinusa istog argumentaі U nizu epizoda jedan od izlagača ( više od koraka sinusa i kosinusa - ovo je treći korak njihovog stvaranja

: ako je trigonometrijska funkcija blizu predznaka integralne jednadžbe, njezin je stupanj negativan. Postoje i vrste privatnih trigonometrijskih funkcija, ako je njihova razina manja od normalne. O njima - sljedeći paragraf. Koliko su prikazi uvredljivi? - dečki, dakle, Vikorist i trigonometrijske formule

smanjite indikatore koraka sinusa i kosinusa, nakon čega dobivate integral istog tipa koji je veći. Stoga integracija traga slijedi isti krug. Znati guza 2.

Ako je jedan od dva pokazatelja negativan, pa se smatra važnijim od ostalih koraka sinusa i kosinusa, tada ova shema nije prikladna

k+ 1 – nespareno. Todi, doktori, što Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene. Zatim je potrebno zamijeniti varijablu u memoriji kako bi se transformirao integralni virus. Takav napad bit će ispitan u sljedećem paragrafu. stražnjica 4. neuparen, zatim ga popravite na sličan način, gledajući multiplikator sin Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene Odluka. ). Todi se može ukloniti

Da se vratimo na staru promjenu, još uvijek znamo

stražnjica 5. Znati guza 2.

.

Odluka.

Indikator kosinusne razine, kao u prvom udarcu, nije uparen ili više. Uyavimo k+ 1 – nespareno. Todi, doktori, što Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene. Zatim je potrebno zamijeniti varijablu u memoriji kako bi se transformirao integralni virus. Takav napad bit će ispitan u sljedećem paragrafu. stražnjica 4. neuparen, zatim ga popravite na sličan način, gledajući multiplikator sin Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene Odluka. ). Todi se može ukloniti

i mi ćemo započeti zamjenu zamjene

Otvaranje hramova

i može se ukloniti

Vraćajući se na staru promjenu, odluka je nestala Znati guza 2.

stražnjica 6.

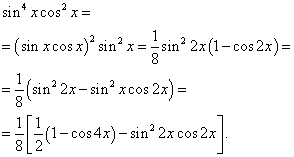
Odluka.

Indikatori razine sinusa i kosinusa - momci. Tako možemo transformirati integralnu funkciju ovako: k Ovo treba odnijeti Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene Za drugi integral, zamijenit ćemo ga drugim, s poštovanjem (1/2)stražnjica 4.= grijeh2 Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene Odluka. . Todi

= cos2

. Otje,

Metoda zamjene Ostatak se može ukloniti Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene = k Vykoristannya metoda zamjene s promjenom Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene = k s integriranim trigonometrijskim funkcijama moguće je zamrznuti u fazama, ako je u integralnom izrazu samo sinus ili samo kosinus, ili sinus i kosinus, ili u sinusu ili u kosinusu - u prvom koraku tangenta ili kotangens, kao i privatni koraci sinusa i kosinusa jednog te istog argumenta. U ovom slučaju, moguće je izvršiti ne samo preuređenje Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene = k unutra je Subintegralni izraz je predstavljen u obliku da je njegov dio funkcija sinusa, ali umjesto toga diferencijal sinusa. Sada za pomoć pri zamjeni promjene = k .

, ali i tg Znati guza 2.

.

ta ctg

.

stražnjica 8. Znati guza 2.

Odluka.

Tražimo zamjenu: , Todi. Integralni virus, koji je superioran, lako se integrira iza tablice integrala: stražnjica 9. Odluka.

.

Tangens novog sinusa i kosinusa je topiv:

.

stražnjica 10 Znati guza 2.

Tražimo zamjenu: , Todi. Integralni izraz, koji jest, jest

stolni integral :

ima znak minus: stražnjica 4. Okrećući se klipu, ostatak se uklanja:

Tangens novog sinusa i kosinusa je topiv:

.

Odluka.

Univerzalna trigonometrijska supstitucija

Tražimo zamjenu: , Todi. Rješiti integralni izraz za utvrđivanje trigonometrijskog identiteta

Moguće je zamijeniti varijablu, ne zaboravite staviti znak minus ispred integrala (iznenadit ćete se da

stražnjica 12 Znati guza 2.

.

). Zatim rastavljamo integralni izraz na množitelje i integriramo ga pomoću tablice: univerzalna trigonometrijska supstitucija Za drugi integral, zamijenit ćemo ga drugim, s poštovanjem
.

Razlomci u brojevniku i knjižici množe se s , a dva se zbrajaju i stavljaju ispred znaka integrala. Todi

Zapravo, često je potrebno izračunati integrale transcendentnih funkcija kao zamjenu za trigonometrijske funkcije. U okviru ovog materijala opisat ćemo glavne vrste integralnih funkcija i pokazati koje se metode mogu koristiti za njihovu integraciju.

Integracija sinusa, kosinusa, tangensa i kotangensa

Naučimo metode integriranja osnovnih trigonometrijskih funkcija - sin, cos, tg, ctg. Koristeći Vikoristovu tablicu primarnih vrijednosti, možemo odmah napisati da je ∫ sin x d x = - cos x + C , i ∫ cos x d x = sin x + C .

Za izračun bezvrijednih integrala funkcija t g i c t g, možete ubrzati predznake diferencijala:

∫ tgxdx = ∫ sin x cos xdx = d (cos x) = - sin xdx = = - ∫ d (cos x) cos x = - ln cos x + C ∫ ctgxdx = ∫ cos x sin xdx = d (sin x) = cos xdx = = ∫ d (sin x) sin x = ln sin x + C

Kako smo izveli formule ∫ d x sin x = ln 1 - cos x sin x + C í ∫ d x cos x = ln 1 + sin x cos x + C, preuzete iz tablice prvih? Objasnimo samo jedan ispad, ali drugi će biti razuman iza analogije.

Koristeći Vikorist metodu supstitucije, pišemo:

∫ d x sin x = sin x = t ⇒ x = a r sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Ovdje trebamo integrirati iracionalnu funkciju. Uzmimo istu metodu zamjene:

∫ dtt 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ dt = - zdz 1 - z 2 = = ∫ - zdzz 1 - z 2 1 - z 2 = ∫ dzz 2 - 1 = ∫ dz (z - 1) (z +) = = 1 2 ∫ dzz - 1 - 1 2 ∫ dzz + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Sada napravimo obrnutu zamjenu z = 1 - t 2 i t = sin x:

∫ dx sin x = ∫ dtt 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

Pogledajmo pobliže razlike s integralima, koji su stupnjevi trigonometrijskih funkcija, kao što su ∫ sin n x d x , ∫ cos n x d x , ∫ d x sin n x , ∫ d x cos n x .

O tome kako ih pravilno izračunati možete pročitati u članku o integraciji s rekurentnim formulama. Ako znate kako izvesti ovu formulu, možete lako integrirati formulu ∫ sin n x · cos m x d x s prirodnim m i n.

Budući da imamo kombinaciju trigonometrijskih funkcija s bogatim terminima ili funkcije prikaza, tada će se morati integrirati u dijelove. Pročitajte članak posvećen metodama pronalaženja integrala ∫ P n (x) · sin (ax) dx , ∫ P n (x) · cos (ax) dx , ea · x · sin (ax) dx , ea · x · cos (ax)dx.

Najsloženiji su zadaci u kojima integralna funkcija uključuje trigonometrijske funkcije s različitim argumentima. Za one koji trebaju znati osnovne formule trigonometrije, važno je zapamtiti ih ili pratiti bilješke pri ruci.

stražnjica 1

Odredite identitet primarnih funkcija y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .

Odluka

Koristeći formule za niži korak, zapisujemo da je cos 2 x 2 = 1 + cos x 2 i cos 2 2 x = 1 + cos 4 x 2. Značiti,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

Znamennik ima formulu sumi sinus. Todi se može napisati ovako:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Imamo zbroj triju integrala.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) dx = = ∫ dx + cos (4 x) dx sin (4 x) + ∫ dx sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

U nekim slučajevima, trigonometrijske funkcije koje su ispod integrala mogu se svesti na racionalnije izraze koristeći jednostavnu metodu standardne supstitucije. Za početak, uzmimo formule koje izražavaju sin, cos i t g kroz tangens pola argumenta:

sin x = 2 t g x 2 1 + t g 2 x 2, sin x = 1 - t g 2 x 2 1 + t g 2 x 2, t g x = 2 t g x 2 1 - t g 2 x 2

Također ćemo morati izračunati diferencijal d x kroz tangentu polusjeka:

Krhotine d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2 tada

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Dakle, sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 pri z = t g x 2.

stražnjica 2

Nađite bezvrijedni integral ∫ d x 2 sin x + cos x + 2 .

Odluka

Vikoristova metoda standardne trigonometrijske supstitucije.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ dx 2 sin x + cos x + 2 = 2 dz 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 dzz 2 + 4 z + 3

Zaključujemo da je ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

Sada možemo rastaviti integralnu funkciju na najjednostavnije razlomke i oduzeti zbroj dvaju integrala:

∫ dx 2 sin x + cos x + 2 = 2 ∫ 2 dzz 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 dz = = ∫ dzz + 1 - ∫ C z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Verzija: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Važno je napomenuti da ove formule koje izražavaju funkcije kroz tangens polovice argumenta nisu identične, budući da izraz ln tgx 2 + 1 tgx 2 + 3 + C nije isti kao primarne funkcije y = 1 2 sin x + cos x + 2 t ilki označena područja.

Za druge vrste zadataka možete koristiti osnovne metode integracije.

Ako ste u tekstu označili uslugu, pogledajte je i pritisnite Ctrl+Enter

Za integraciju racionalnih funkcija oblika R(sin x, cos x) upotrijebite zamjenu koja se naziva univerzalna trigonometrijska zamjena. Todi. Univerzalna trigonometrijska zamjena često dovodi do izvrsnih izračuna. Stoga, u mjeri u kojoj je to moguće, može se profitirati od takvih zamjena.

Integracija funkcija koje racionalno leže unutar trigonometrijskih funkcija

1. Integrali oblika ∫ sin n xdx , ∫ cos n xdx , n>0
a) Ako n nije uparen, tada se pod predznakom diferencijala treba unijeti jedan korak sinx (ili cosx), a iz uparenog koraka sljedeći korak premjestiti na suprotnu funkciju.
b) Ako ste muškarac, onda možete koristiti formule niže razine
2. Integrali oblika ∫ tg n xdx , ∫ ctg n xdx , gdje je n cjelina.
Potrebno je ispraviti formule

3. Integrali oblika ∫ sin n x cos m x dx
a) Otpustite m i n različitih parova. Pretpostavljamo zamjenu t = sin x, ako je n nesparen ili t = cos x, ako je m nesparen.
b) Ako su m i n dečki, tada se koriste formule niže razine
2sin 2 x=1-cos2x, 2cos 2 x=1+cos2x.
4. Integrali oblika
Budući da su brojevi m i n istog para, koristimo zamjenu t=tg x . Često je teško ručno koristiti trigonometrijsku jedinicu.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Najbrže formule za pretvaranje stvaranja trigonometrijskih funkcija na njihov zbroj:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Nanesite ga
1. Izračunajte integral ∫ cos 4 x · sin 3 xdx.
Zamijenimo cos(x)=t. Todi ∫ cos 4 x sin 3 xdx =
2. Izračunajte integral.
Robly zamjena sin x = t, eliminirana

3. Nađi integral.
Zamijenimo tg (x) = t. Zamjenska, uklonjiva

Integracija izraza u obliku R(sinx, cosx)

Guzica #1. Izračunajte integrale:

Odluka.
a) Integracija izraza u obliku R(sinx, cosx), gdje je R racionalna funkcija u obliku sin x i cos x transformiraju se u integrale u obliku racionalnih funkcija uz pomoć univerzalne trigonometrijske supstitucije tg(x) /2) = t.
Todi mayo

Univerzalna trigonometrijska supstitucija omogućuje prijelaz s integrala oblika ∫ R(sinx, cosx) dx na integral u razlomačko-racionalne funkcije, ali često takva zamjena dovodi do glomaznih izraza. Za raspjevane umove učinkovite su jednostavne zamjene:

• Ako jednakost R(-sin x, cos x) = -R(sin x, cos x) dx prestane, tada zamjena cos x = t postaje stabilna.
• Ako je jednadžba jednaka R(sin x, -cos x) = -R(sin x, cos x) dx, tada je supstitucija sin x = t.
• Ako je jednadžba jednaka R(-sin x, -cos x) = R(sin x, cos x) dx, tada je supstitucija tgx = t ili ctg x = t.

Koja je metoda za pronalaženje integrala?
uspostavljena je univerzalna trigonometrijska supstitucija tg(x/2) = t.
Todi Vidpovid: